A B C D E F G H I JKL MN O P Q R S T UV WXYZ
Algebra 2 Connections Glossary
undoing   
  Using inverse operations and reversing the order of operations to solve an equation in one variable or to “undo”  a function rule in order to write its inverse.  For example, in the equation y = x3 − 7, add y and write the cube root.  (pp. 222, 263, 264)
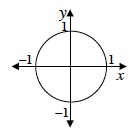
unit circle   
  A circle with a radius of  one unit is called a unit circle.  (pp. 390, 402)

pic
variable   
  A symbol used to represent one or more numbers.  In this course, letters of the English alphabet are used as variables in addition to the Greek letters, θ, a, and pic.  (p. 38)
vertex   
  For a parabola that is a function, the vertex of a parabola is the lowest or highest point of the graph of the parabola.  The vertex of a parabola locates its position with respect to the axes.  It is the lowest or highest point of the graph of the parabola.  In general, the vertex is the turning point for a graph.  (p. 168)  See “parabola,” “ellipse,” “hyperbola,” “absolute value,” for other graphs with vertices (the plural of vertex). 

pic
vertex form   
  The vertex form for the equation of a quadratic function (also called graphing form) is written  y = a(x − h)2 + k.  (p. 177)
vertical shift   
  Used to describe the location of a graph in relation to its parent graph, the shift is the vertical distance (up or down) of each point on the graph from the corresponding point on the parent graph.  For example, each point on the graph of y = x2 + 2 is two units higher that its corresponding point on y = x2.  In a general equation such as y = a(x − h)2 + k the vertical shift is represented by k.  (p. 175) 

pic
volume  
  For a 3-dimensional figure the number of non-overlapping cubic units that will fit inside.  (p. 25)