factor
Factor Theorem
factorial
n! = n(n− 1)(n − 2)(n − 3) ·... · 3 · 2 · 1 For example, 5! = 5 · 4 · 3 · 2 · 1 = 120. (pp 515, 521)
fair game
| A | B | C | D | E | F | G | H | I | JKL | MN | O | P | Q | R | S | T | UV | WXYZ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algebra 2 Connections Glossary | ||||||||||||||||||
factor |
|
|---|---|
| A factor is part of a product. A polynomial expression p(x) is a factor of another polynomial expression P(x) when there is a polynomial q(x)such that p(x)q(x) = P(x). In the equation 3x2 − 9x + 6 = 3(x − 2)(x −1), the expressions (x − 2), (x − 1) and 3 are factors. (pp. 23, 149, 475) | |
Factor Theorem |
|
| States that if a is a root of a polynomial then x − a is a factor, and if x − a is a factor then a is a root. For example, the polynomial x2 − 5x − 6 = (x − 6)(x + 1) and the roots are 6 and –1. | |
factorial |
|
| A shorthand notation for the product of a list of consecutive positive integers from the given number down to 1: n! = n(n− 1)(n − 2)(n − 3) ·... · 3 · 2 · 1 For example, 5! = 5 · 4 · 3 · 2 · 1 = 120. (pp 515, 521) |
|
fair game |
|
| A game in which the expected values for each player are equal. If you pay to play a game then the game is fair if the cost to play equals the expected value. For example, player A and player B are rolling a die to see how far to move in a board game. If the die comes up 1, 2, 3, or 4, player A moves that many spaces. If the die comes up 5 or 6 player B gets to move that many spaces. Player A has an expected value of moving | |
family of functions |
|
|---|---|
| A group of functions that have at least one common characteristic. For example we describe all cubic functions, y = a(x − h)3 + kas the family of functions with parent graph y = x3 . All are cubic polynomials and all of the graphs are similar in shape. The set of all equations y = mx + 7 describes the family of linear functions with y-intercept 7. (pp. 189, 207) | |
feasible region |
|
Used to describe the intersection of the graphs of a set of inequalities that represent the constraints or parameters of a problem situation. The feasible region represents the points with coordinates that satisfy the given conditions. (pp. 241, 245)
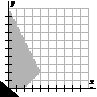
|
|
focal length |
|
| The distance c from the vertex to the focus of a parabola is called the focal length. In a hyperbola or an ellipse focal length is the distance c, from the center to one focus. See “focus of a parabola,” “foci of an ellipse,” and “foci of a hyperbola.” (p. 568) | |
foci of an ellipse |
|
| Every ellipse has two points on its major axis called the foci of the ellipse. For any point (x, y) on the ellipse, the sum of the distances from each focus to (x, y) is a constant. An ellipse with its center at the origin, x-intercepts of (±a, 0) and y-intercepts (0, ±b), where a > b, has its foci at (±c, 0), with c2 = a2 − b2. When the center is (0, 0) and the major axis is on the y‑axis the foci are (0,±c). (pp. 570, 571) See “ellipse. “ | |
foci of a hyperbola |
|
| Each hyperbola has two points on its transverse axis called the foci of the hyperbola. For any point (x, y) on the hyperbola, the difference between the distances from each focus to (x, y) is constant. A hyperbola with it center at the origin, x-intercepts (±a, 0) and asymptotes |
|
focus of a parabola |
|
| A parabola is defined to be the set of points in the plane, each of which is the same distance from a fixed point (the focus) as it is from a fixed straight line (the directrix). Also, if rays parallel to the line of symmetry enter into the interior of the parabola to intersect the parabola and reflect so that the angle of incidence equals the angle of reflection, then all such rays intersect at the focus of the parabola. (pp. 556, 568) See “parabola.” | |
fractional exponents |
|
| Raising a number to a fractional exponent indicates a power as well as a root. |
|
function |
|
| A relationship in which for each input there is exactly one output. For example, y = x2 is a function because each input for x determines one output. x2 + y2 = 25 is not a function, because, for example, when x = 4 , y could be either 3 or –3. (pp. 6, 197, 199) | |
function notation |
|
| A convenient way to represent a function or to write a rule to show what a function machine does is to name the function with a letter and put the variable that represents the inputs in parentheses, for example f ( ) . When the variable is x, this will be f(x) . Read it “f of x” to mean the output of the function when the operations of f are performed on the input x. (p. 231) | |
f−1(x) |
|
|---|---|
| Read this as “f inverse of x,” the inverse function for f(x) . (p. 231) | |