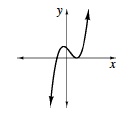
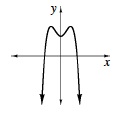
| Used informally in this course to describe some graphs. For example the direction a parabola opens might be referred to as its orientation. When describing the graph of a polynomial function, a positive orientation would mean the graph eventually continues upward as the value of x increases, as in the example above right. A negative orientation would mean it eventually heads downward as the value of x continues to increase, as in the example below right. (pp. 175, 445)
|
|
outcome |
|
| Used to describe the result of an event in counting and probability problems. For example, when rolling one six-sided die, the possible outcomes are the numbers 1, 2, 3, 4, 5, and 6. (pp. 497, 502, 510) | |
output |
|
| Used to describe the result of applying a function or relationship rule to an input value. When a function is represented by a function machine the output is the number that comes out of the machine. For the function f(x) = x2 − 73 when the input is 10, the output is 27. Function notation shows how the function operates on the input to produce the output: f(10) = 102 − 73 = 27. (p. 6) | |