Pascal's Triangle
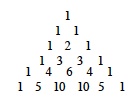
percentile
perfect square
| A | B | C | D | E | F | G | H | I | JKL | MN | O | P | Q | R | S | T | UV | WXYZ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algebra 2 Connections Glossary | ||||||||||||||||||
parabola |
|
|---|---|
| The set of all points that are equidistant from a single point (the focus) and a line (the directrix). The general equation for a parabola that is a function (or a quadratic function) in graphing (or vertex) form, is y = a(x − h)2 + k. The general equation of a quadratic function in standard form is y = ax2 + bx + c. A general equation for parabolas that are not functions, “sleeping” parabolas, is x − h = a(y − k)2. (pp. 168, 171, 179, 181‑183, 199, 555, 556, 568) | |
parallel |
|
| Two lines in a plane are parallel if they never intersect. Parallel lines have the same slope. Two line segments in a plane are parallel if the lines they lie on lines that never intersect. Two lines in space are parallel if they lie in the same plane and they do not intersect. There is a constant distance between parallel lines. | |
parameter |
|
| In a general equations where x and y represent the inputs and outputs of the function, variables such as a, b, c, m, h, and k are often referred to as parameters, and they are often replaced with specific values. For example: in the equation y = a(x − h)2 + k representing all parabolas that are functions, the a, h, and k are (variable) parameters that give the shape and location, while x and y are the independent and dependent variables. (pp. 38, 115, 143, 175, 413) | |
parent graph |
|
| The simplest version of a family of graphs. For instance, the graph of y = x2, is considered the parent graph for parabolas that are functions. (p. 182)
|
|
Pascal's Triangle |
|
| The array of numbers at right. The triangular pattern continues downward. This array shows all the values of nCr where n is the row number when the vertex is 0C0. r is the number of places to the right in row n (when the counting begins with 0). For instance, 5C2is equal to 10. (p. 649)
|
|
percentile |
|
| A percentile ranking indicates the percentage of scores which are below the score in question. For example, if you scored at the 90th percentile on a test, your score was higher than the scores of 90% of the other test takers. | |
perfect square |
|
| Usually, a quadratic polynomial ax2 + bx + c that can be rewritten as the second power of a binomial, (cx + d)2. For example, x2 − 6x + 9 is a perfect square that can be rewritten as (x − 3)2. Also, any polynomial of even degree that can be rewritten as the square of one polynomial factor. For numbers, a whole number that can be written as the second power of another whole number. For example, 1, 4, 9, 16, and 25 are perfect squares. | |
perimeter |
|
| The distance around the exterior of a figure on a flat surface. For a polygon the perimeter is the sum of the lengths of its sides. The perimeter of a circle is called its circumference. | |
period |
|
| The length of one cycle of a graph, as shown by the dashed line in the graph below. (pp. 416, 423)
|
|
periodic function |
|
|---|---|
| A function which has a repetitive section or cycle such as the sine, cosine and tangent functions. In a periodic function, the cyclic pattern continues forever both to the left and to the right. (p. 423) | |
permutation |
|
| A permutation is an arrangement in which the order of selection matters. For example a batting line-up is a permutation because it is an ordered list of players. If each of five letters, A, B, C, D, E is printed on a card, the number of 3-letter sequences can you make by selecting three of the five cards is a permutation. Permutations can be represented with tree diagrams, decision charts, and their value calculated by using the formula for |
|
perpendicular |
|
| Two lines, rays, or line segments that intersect to form a right angle. A line and a plane can also be perpendicular if the line does not lie in the plane, but intersects it and forms a right angle with every line in the plane that passes through the point of intersection. | |
plane |
|
| A plane is an undefined term in geometry. It is a two‑dimensional flat surface that extends without end. It is made up of points and has no thickness. The part of a plane outlined by its xy-, xz- and yz‑traces is often used to represent a plane on a 3‑dimensional coordinate system. (pp. 312, 320) | |
point |
|
| An undefined term in geometry. A point has no dimensions but can be located by its coordinates on a number line, in a plane, or in space. | |
point-slope form |
|
| y − k = m(x − h) is called the point slope form of a linear equation or function because it shows the slope m and a point (h, k) that is on the graph of the line. For example, given a line that has slope |
|
polynomial |
|
| An algebraic expression that involves at most the operations of addition, subtraction, and multiplication. A polynomial in one variable is an expression that can be written as the sum of terms of the form: |
|
Power Property of Logs |
|
| logm(an) = nlogm(a). For example, log3625 = 4log35. (pp. 330, 335) | |
principal |
|
| Initial investment or capital. An initial value. | |
probability |
|
|---|---|
| The probability that an event A. with a finite number of equally likely outcomes, will occur is the number of outcomes for event A divided by the total number of equally likely outcomes. This can be written as |
|
Product Property of Logs |
|
| logm(a · b) = logm(a) + logm(b). For example, log330 = log35 + log36 . (p. 334) | |
profit |
|
| The amount of money after expenses have been accounted for. (pp. 241, 242, 245) | |
proof by induction |
|
| (pp. 629, 632) See “mathematical induction.” | |
proportion |
|
| Equal ratios are described as a proportion. For example, the equation |
|
Pythagorean Identity |
|
| For trigonometric functions, cos2x + sin2x = 1 for any value of x. (pp. 689, 695) | |