A2C Glossary

A	B	C	D	E	F	G	H	I	JK L	MN	O	P	Q	R	S	T	UV	WXYZ
Algebra 2 Connections Glossary

sample space
	With probability, all the possible outcomes. (pp. 501, 510)
secant
	The reciprocal of the cosine. (p. 683)
sequence
	A function in which the independent variable is a positive integer (sometimes called the “term number”). The dependent variable is the term value. A sequence is usually written as a list of numbers. For example, the arithmetic sequence 5, 8, 11, … (pp. 69, 71, 83)
series

sigma
	The sum of the terms of a sequence. (pp. 610, 618, 636)
	The Greek letter which is used to mean sum. Using provides a way to write a short, compact mathematical representation for a series. (p. 626) See “summation notation.”
similar
	Two figures are similar if they have the same shape, but are not necessarily the same size. The ratios of the lengths of corresponding sides of similar figures are equivalent.
simple interest

simplify
	Interest paid on the principal alone. (p. 125)
	To rewrite an expression or equation as an equivalent expression or equation in a form that is considered to be simpler or less cumbersome than the original. (p. 133) See “rewrite.”
sine
	In a right triangle (as shown below) the ratio is known as the sine of the acute angle. Below,since the side length b is opposite angle B. (p. 407)

sine function
	For any real number θ, the sine of θ,, denoted sinθ,, is the y‑coordinate of the point on the unit circle reached by a rotation angle of θ, radians in standard position. The general equation for the sine function is y = a sin b(x − h) + k. This function has amplitude a, period , horizontal shift h, and vertical shift k. (pp. 383, 409, 423)
sine inverse
	(sin−1 x) Read as the inverse of sine x, sin⁻¹x is the measure of the angle with sine x. We can also write y = arcsin x . Note that the notation refers to the inverse of the sine function, not . Because y = sin⁻¹x is equivalent to x = sin y and there are infinitely many angles y such that sin y = x , the inverse function is restricted to select the principal value of y such that . The graph of the inverse function, y = sin⁻¹x with is below. (p. 684)
sketch
	To sketch the graph of an equation means to show the approximate shape of the graph in the correct location with respect to the axes with key points clearly labeled. (p. 8)
“sleeping” parabola

slope
	A “sleeping” parabola is a parabola which opens to the left or right, rather than upward or downward. These parabolas are not the graphs of functions. (p. 199)
	The ratio of the vertical change to the horizontal change between any two points on a line. For any two points (x₁, y₁) and (x₂, y₂) on a given line, the slope is . For example, the slope of a line between points with coordinates (3, −5) and (−7, 2) is . (pp. 11, 200)
slope-intercept form
	A linear equation written in the form y = mx + b is written in slope‑intercept form. In this form, m is the slope of the line and the point (0, b) is the y-intercept. (p. 11)

standard form (quadratic relations in general)
	The standard for parabolas, ellipses, and hyperbolas with axes parallel to the x- or y-axes is Ax² + By² + Cx + Dy + E = 0. (p. 593)
standard window
	The graphing window on a calculator set to show the x- and y-axes for values −10 ≤ x ≤ 10 and −10 ≤ y ≤ 10.
stretch factor
	Used to describe the effect of a in the graphing form of a quadratic, cubic, absolute value, or exponential function. For a > 1 or a < − 1 the outputs increase or decrease faster than the outputs for the parent functions, and the graphs are described as being stretched upwards or downwards in relation to the parent graph. (pp. 170, 175)
subproblems

substitution
	A large problem can sometimes be separated into smaller or simpler problems called “subproblems” so that the solution of these subproblems leads to the solution of the larger problem. (p. 529)
	Replacing a variable or expression with a number, another variable, or another expression. For example, when evaluating the function f(x) = 5x − 1, for x = 3, substitute 3 for x to get f(3) = 5(3) − 1 = 14 . (p. 56)
substitution to solve a system of equations
	A method for solving a system of equations by replacing one variable with an expression involving the remaining variable(s). (p. 56)
summation notation

surface area
	A convenient way to represent a series is to use summation notation. The Greek letter sigma, 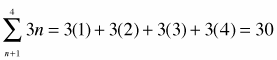, indicates a sum. For example, . The numbers below and above the sigma are called the indices. The index below, n = 1, tells us what value to start with for n. The top index tells us how high the value can go. In the example shown above, n starts at 1 and increases to 4. (pp. 626, 627)
	The sum of all the areas of the surfaces of a three-dimensional figure or object.
symmetry
	A figure that appears not to change when reflected across a line is said to have reflection symmetry. A figure that appears not to change when rotated through an angle of less than 360º is described as having rotation symmetry. (p. 167)
system of equations

	A system of equations is a set of equations with more than one unknown or variable. The systems we solve most often in this course have two or three equations and two or three variables. Systems of equations are often solved using substitution or elimination to reduce the number of variables. A system of quadratic equations is shown at right. (pp. 17, 223, 224, 229,232, 250 )