identity (trigonometric)
identity element
identity matrix
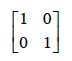
imaginary numbers
| A | B | C | D | E | F | G | H | I | JKL | MN | O | P | Q | R | S | T | UV | WXYZ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algebra 2 Connections Glossary | ||||||||||||||||||
identity (trigonometric) |
|
|---|---|
| Equations that are true for all values for which the functions are defined. For example sin2 x + cos2 x = 1 which is true for all values of x, or |
|
identity element |
|
| The identity element for addition is the number we can add to any number and not change that number’s “identity” or value. For addition, the identity element is 0; a + 0 = a for any number, a. For multiplication, the identity element is 1, because 1 − x = x for any number x. (p. 362) | |
identity matrix |
|
| An m by m matrix, often labeled I, with zero in every entry except those on the upper‑left to lower‑right diagonal. On that diagonal, each entry mij = 1. For any m by m matrix, M, MI = IM = M . The identity matrix for a 2 by 2 matrix is shown below. (p. 362)
|
|
imaginary numbers |
|
| The set of numbers that are solutions of equations of the form x2 = (a negative number) are called imaginary numbers. They are not positive, negative, or zero. The imaginary number i is a solution of the equation x2 = − 1, so i−2 = − 1. In general, imaginary numbers follow the rules of real number arithmetic (e.g. i + i = 2i ). Multiplying the imaginary number i by every possible real number yields all possible imaginary numbers. (pp. 454, 456) | |
independent events |
|
| When the probability of two events happening equals the product of their probabilities, the events are said to be independent. For example, the probability of landing on red on two consecutive spins of a roulette wheel is |
|
independent variable |
|
| In a function, the independent variable is the input variable. The variable occurring first in an ordered pair. (pp. 6, 13, 199) | |
index (plural indices) |
|
In summation notation, the indices are the numbers below and above the sigma that indicate which term to start with and which to end with. For a series they show the first and last replacement values for n. When the symbol above sigma is ∞ the series continues without ending. Example: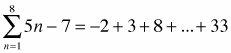 . (pp. 626, 627) . (pp. 626, 627) |
|
inequality |
|
| A mathematical statement that shows a relationship between two values or expressions where one is greater than (>) the other, or less than (<) the other, or just not equal (≠) to the other. (p. 243) | |
inequalities with absolute value |
|
| If k is any positive number, an inequality of the form: |f(x)| > k is equivalent to the statement f(x) > k or f(x) < −k; and |f(x)| < k is equivalent to the statement −k < f(x) < k. For example, you can solve the inequality, |5x − 6| > 4by solving the two inequalities 5x − 6 > 4 or 5x − 6 < −4. (p. 243) | |
infinite geometric series |
|
|---|---|
| An infinite geometric series is a geometric series which never ends. The sum of such a series with an initial value a and common ratio r, with −1 < r < 1, is given by the formula below. (p. 647)
|
|
inflection point |
|
A point at which a graph changes concavity. Concavity refers to whether the graph opens upward or downward. So an inflection point is a point at which a graph changes from opening upward to opening downward, or vice versa. The graph of y = x3 has an inflection point, otherwise known as a point of inflection, at x = 0. |
|
initial ray |
|
| When an angle of rotation is drawn in standard position, the positive x-axis is called the initial ray. (p. 403) See “angle and angle of rotation.” | |
initial value |
|
| The initial value of a sequence is the first term of the sequence. (pp. 69, 86) | |
input |
|
| A replacement value for a variable in a function or relation. The first number in an ordered pair. The set of all possible input values is the domain of a function. (p. 6) | |
integer |
|
| Any whole number or the opposite of a whole number ...− 3, − 2, −1, 0, 1, 2, 3,... (p. 475) | |
integral roots |
|
| Roots (or zeros) of functions that are integers. (p. 475) | |
intercepts |
|
| Points where a graph crosses the axes. x-intercepts are points at which the graph crosses the x axis and y-intercepts are points at which the graph crosses the y axis. On the graph below the x-intercept is (3, 0) and the y-intercept is (0, 6). (p. 11)
|
|
interest |
|
| An amount paid which is a percentage of the principal. For example, a savings account may offer 4% annual interest rate, which means they will pay $4.00 in interest for a principal of $100 kept in the account for one year. (p. 125) | |
intersection |
|
|---|---|
A point of intersection is a point that the graphs of two or more equations have in common. Graphs may intersect in one, two, several, many or no points. The set of coordinates of a point of intersection are a solution to the equation for each graph. (pp. 17, 21, 222, 223, 224)
|
|
inverse circular functions |
|
| See “inverse trigonometric functions.” (p. 684) | |
inverse function |
|
| A function that “undoes” what the original function does. It can also be seen as the x-y interchange of the function. The inverse of a function performs in reverse order the inverse operation for each operation of the function. The graph of an inverse function is a reflection of the original function across the line y = x . For example, y = x3 + 2 is equivalent to
|
|
inverse operations |
|
| Subtraction is the inverse operation for addition and vice versa, division for multiplication, square root for squaring, and more generally taking the nth root for raising to the nth power. | |
inverse trigonometric functions |
|
| For each trigonometric function sin(x), cos(x), and tan(x) , there is an inverse function written sin−1(x), cos−1(x), and tan−1(x). Note: this symbol does not mean |
|
investigating a function |
|
| To investigate a function means to make a complete graph of the function and to write down everything you know about the function. Some things to consider are: domain, range, intercepts, asymptotes, inverse, and symmetry. (p. 32, 34) | |
isosceles triangle |
|
| A triangle with two sides of equal length. | |
isometric dot paper |
|
| Useful for graphing three dimensional figures. The pattern of dots on the paper enhances the 3-dimensional appearance of the x-, y-, and z-axes. (p. 308) | |