major axis
mathematical induction
matrix
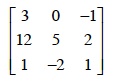
maximize
| A | B | C | D | E | F | G | H | I | JKL | MN | O | P | Q | R | S | T | UV | WXYZ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algebra 2 Connections Glossary | ||||||||||||||||||
major axis |
||
|---|---|---|
| The longer axis of an ellipse. The distance from the center of the ellipse to the end of the major axis is the semi-major axis, represented as a in the general equation. (pp. 574, 576) See “ellipse.” | ||
mathematical induction |
||
| In this course, a method of proof that can be used to prove that a formula is true for any natural number (n = 1, 2, 3, ….) Such a proof consists of the following steps: (i) Verify that the formula is true for n = 1. (ii) Write the general statement of the formula for n = k+1. (iii) Show and justify the reasoning needed to move from the result for n = k to get to the next case where n = k + 1 . (pp. 629, 632) | ||
matrix |
||
| A rectangular array of numbers or algebraic expressions enclosed in square brackets.
|
||
maximize |
||
| Make as large as possible. (pp. 242, 246) | |
maximum point |
|
| The highest point on a graph. For example, the vertex of a downwardly oriented parabola. (pp. 242, 246) | |
maximum value |
|
| The largest value in the range of a function. For example, the y-coordinate of the vertex of a downwardly oriented parabola. (pp. 242, 246) | |
mean |
|
| The average for a set of data. The mean is found by summing all the numbers and dividing the sum by the number of pieces of data. (p. 94) | |
median |
|
| The middle score of a set of data. The median is found by arranging the numbers from highest to lowest and finding the number in the middle. If the number of values is even, the median is the average (mean) of the two middle numbers. (p. 94) | |
minimize |
|
| Make as small as possible. (pp. 242, 246) | |
minimum point |
|
|---|---|
| The lowest point on a graph. For example, the vertex of an upwardly oriented parabola. (p. 242, 246) | |
minimum value |
|
| The smallest value in the range of a function. For example, the y‑coordinate of the vertex of an upwardly oriented parabola. (pp. 242, 246) | |
minor axis |
|
| The shorter axis in an ellipse. The length of the semi-minor axis, the distance from the center to the end of the minor axis, is represented by b in the general equation. (pp. 574, 576) See “ellipse.” | |
multiplicative inverse |
|
| The multiplicative inverse for a non-zero number is the number we can multiply by to get the multiplicative identity, 1. For example, for the number 5, the multiplicative inverse is |
|
multiplicative inverse |
|
| The multiplicative inverse for a non-zero number is the number we can multiply by to get the multiplicative identity, 1. For example, for the number 5, the multiplicative inverse is |
|
multiplier |
|
| In a geometric sequence the number multiplied times each term to get the next term is called the multiplier or the common ratio or generator. The multiplier is also the number you can multiply by in order to increase or decrease an amount by a given percentage in one step. For example, to increase a number by 4%, the multiplier is 1.04. We would multiply the number by 1.04. The multiplier for decreasing by 4% is 0.96. (pp. 79, 80, 83, 86) | |
negative exponents |
|
| Raising a number to a negative exponent is the same as taking the reciprocal of the number. |
|
non-function |
|
| A relation that has more than one output for one or more of its inputs. (pp. 197, 198) | |