3-dimensional coordinate system |
| |
In three dimensions the z‑axis is perpendicular to the x‑y plane at (0, 0). Points in 3‑dimensions are represented with coordinates (x, y, z). The first octant where x,‑y, and‑z are positive is shown at right with the point (2, 3, 1). (p. 307) |
absolute value |
| |
The absolute value of a number is the distance of the number from zero. Since the absolute value represents a distance without regard to direction, it is always a positive real number. For example, |−7| = 7, and |7| = 7. The absolute value of a complex number is its distance from zero in the complex plane. For a complex number a + bi, 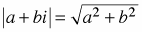 . For example, . For example, 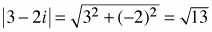 . (pp. 193, 464, 466) . (pp. 193, 464, 466) |
additive identity |
| |
The number 0 is called the additive identity because adding 0 to any number does not change the number. An additive identity matrix or 0 matrix is a matrix of all 0’s. (pp. 352, 362)
|
additive inverse |
| |
The additive inverse of a number is the number we can add to that number to get the additive identity, 0. So, for the number 5, the additive inverse is −5; for the number −13, the additive inverse is 13. For any number x, the additive inverse is −x. (p. 352)
|
algebraic representation |
| |
Algebraic representation generally means representing the mathematical relationships using numbers, a variable or variables, and operation symbols in equations, or inequalities.
|
algebraic strategies |
| |
Using algebraic strategies means to write an algebraic representation of the problem and then to rewrite those expressions to get equivalent, but more useful results that lead to a solution for the problem or that reveal more information to help solve it. (pp. 221, 224) |
amplitude |
| |
The amplitude of a cyclic graph is one‑half the distance between the highest and lowest points. In the graph at right, a is the amplitude. (pp. 421, 423)
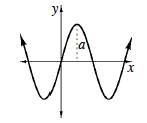 |
angle |
| |
An angle is formed by two rays joined at a common endpoint (the vertex). In geometric figures, angles are usually formed by two segments with a common endpoint.
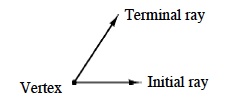
|
angles of rotation. |
| |
Angles with one vertex at the origin and formed by counter-clockwise rotation from the positive x‑axis, are referred to as angles of rotation in standard position. For an angle θ, in standard position, the positive x‑axis is the initial ray and the terminal ray may point in any direction. The measure of such an angle may have any real value. (p. 403)
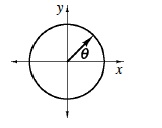
|
appreciation |
| |
An increase in value. (p. 151) |
arccosine of x |
| |
See “cosine inverse (cos−1x).” (pp. 675, 679) |
arcsine of x |
| |
See “sine inverse (sin−1x).” (p. 678) |
arctangent of x |
| |
See “tangent inverse (tan−1x).” (p. 679) |
area |
| |
For a 2‑dimensional region, the number of non-overlapping square units needed to cover the region. Also see “surface area.” |
area model |
| |
An area model or diagram is one way to represent the probabilities of the outcomes for a sequence of two events. The total area is one, and the probabilities are represented by proportional parts. In the example, P(S) and P(not S) are the dimensions of the right side. The probabilities that A will occur or not occur depending on when S occurs are the top and bottom of the rectangle. The area of each part is the probability of each possible sequence of two events. (p. 502)
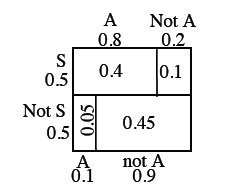
|
argument |
| |
Used with sigma notation for sequences to describe the nth term. In the expression, 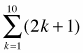 the expression 2k + 1 is the argument. (p. 627) the expression 2k + 1 is the argument. (p. 627) |
arithmetic sequence |
| |
In an arithmetic sequence the difference between sequential terms is constant. Each term of an arithmetic sequence can be generated by adding the common difference to the previous term. For example in the sequence, 4, 7, 10, 13, …, the common difference is 3. (pp. 71, 75, 83) |
arithmetic series |
| |
An arithmetic series is the sum of the terms of an arithmetic sequence. Given the arithmetic sequence 3, 7, 11,...43, the corresponding arithmetic series is 3 + 7 + 11 +...+ 43. . (pp. 610, 618, 622) |
arrange, arrangement |
| |
We arrange a set of objects or make an arrangement when we put them in a particular order, in a line, in a row, around a circle, on a shelf, in a stack, around a table… (pp. 523, 525, 530) |
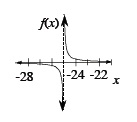
asymptote |
| |
A line that the graph of a curve approaches so that the distance between the graph and the line gets as small as you wish. We often graph functions, which have vertical and/or horizontal asymptotes. For example the asymptotes for the graph of 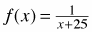 are x = −25 and y = 0. are x = −25 and y = 0.
(Asymptotes are more completely defined in later courses.) (pp. 116, 118, 181, 183, 289)
|
axes |
| |
In a coordinate plane, the two perpendicular number lines that intersect at the origin (0, 0). The x-axis is horizontal and the y-axis is vertical. In 3‑dimensions a third number line, the z‑axis is perpendicular to the x‑y plane at the origin (0, 0, 0). (p. 307) See“coordinate axes” and “3‑dimensional axes” for illustration. |




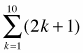 the expression 2k + 1 is the argument. (p. 627)
the expression 2k + 1 is the argument. (p. 627)