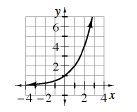
| |
The eccentricity of an ellipse is a measurement reflecting its “roundness. The eccentricity, e, is found with the formula 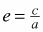 , where c2 = a2 − b2, and a and b are the lengths of the semi-major and semi-minor axes. For a hyperbola, the eccentricity is a measure of the shape of the curve; the larger the eccentricity the more quickly the branches spread apart. The formula is also , where c2 = a2 − b2, and a and b are the lengths of the semi-major and semi-minor axes. For a hyperbola, the eccentricity is a measure of the shape of the curve; the larger the eccentricity the more quickly the branches spread apart. The formula is also 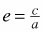 . Note that since c > a, the eccentricity of a hyperbola is always greater than 1; ellipses have eccentricity less than 1. Parabolas have eccentricity equal to 1, and circles have eccentricity equal to 0. (pp. 576, 585) . Note that since c > a, the eccentricity of a hyperbola is always greater than 1; ellipses have eccentricity less than 1. Parabolas have eccentricity equal to 1, and circles have eccentricity equal to 0. (pp. 576, 585) |
| |
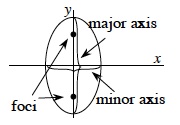
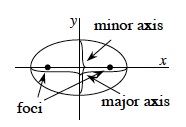
The set of all points for which the sum of their distances from two fixed points, the foci, remains constant. You can visualize an ellipse as a circle that has been stretched vertically or horizontally. The general form of the equation of an ellipse (with a horizontal major axis) is 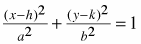 . The line through the two vertices of the ellipse in the long direction is called the major axis of the ellipse, and the distance from the center of the ellipse to one end of the major axis is called the semi‑major axis. The shortest length across the center of the ellipse is the minor axis, and half this length is the semi-minor axis. If a is the length of the semi-major axis, b the semi minor axis, c the distance from the center to either focus, and (h, k) is the center, then the equation of the ellipse can be written . The line through the two vertices of the ellipse in the long direction is called the major axis of the ellipse, and the distance from the center of the ellipse to one end of the major axis is called the semi‑major axis. The shortest length across the center of the ellipse is the minor axis, and half this length is the semi-minor axis. If a is the length of the semi-major axis, b the semi minor axis, c the distance from the center to either focus, and (h, k) is the center, then the equation of the ellipse can be written
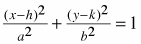 , if the major axis is horizontal or , if the major axis is horizontal or
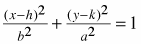 , if the major axis is vertical. , if the major axis is vertical.
In either case, b is defined by c2 = a2 − b2, and the eccentricity is 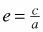 . (pp. 570, 571, 575, 576) . (pp. 570, 571, 575, 576) |

![]() . (pp. 570, 571, 575, 576)
. (pp. 570, 571, 575, 576)